二分查找模板

一、整数二分
- 1.1 整数二分查找模板
  - 1.1.1 寻找右边界的二分查找
  - 1.1.2 寻找左边界的二分查找
二、浮点数二分
- 2.1 浮点数二分查找模板
三、使用STL进行二分查找

一、整数二分

二分查找分为整数二分和浮点数二分，一般所说的二分查找都是指整数二分。

1.1 整数二分查找模板

满足单调性的数组一定可以使用二分查找，但可以使用二分查找的数组不一定需要满足单调性。

不妨假设我们找到了条件 \(C_1\)，它和它的 对立条件 \(C_2\) 能够将数组 \(a\) 一分为二，如下图所示：

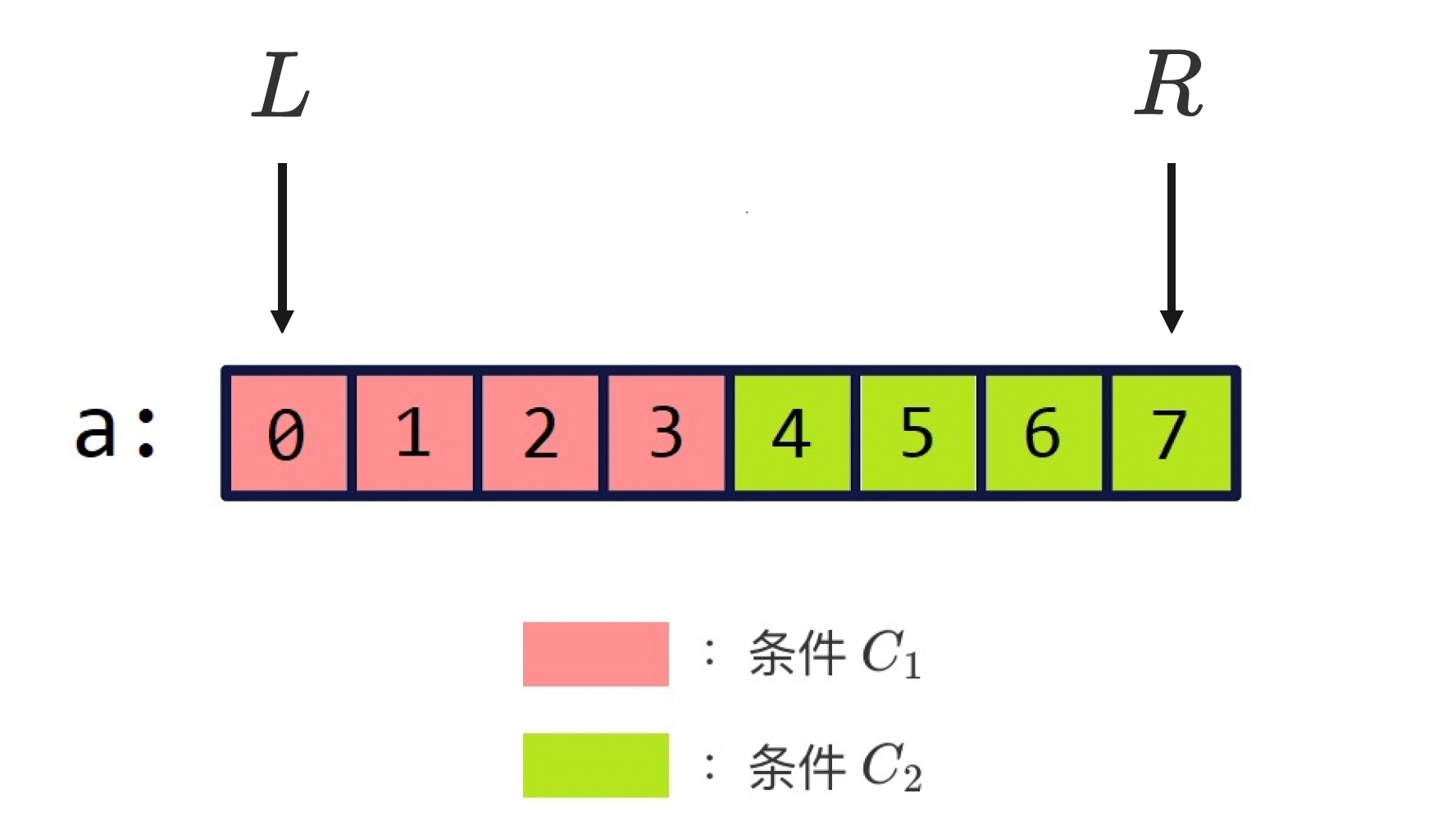
因为 \(C_1\) 和 \(C_2\) 互为对立，故总有 \(C_1\cup C_2\equiv \text{True}\)，\(C_1\cap C_2\equiv \text{False}\)（用C++语言描述，就是 c1 || !c1 总是为真，c1 && !c1 总是为假）。换句话说，\(\forall \,x\in a\)，\(x\) 至少满足 \(C_1\) 和 \(C_2\) 中的一个，且 \(x\) 不会同时满足 \(C_1\) 和 \(C_2\)。

观察上图可以发现，索引3和索引4这两个位置都可以作为\(C_1\)和\(C_2\)的分界点。其中，索引3是红色区域的右边界，索引4是绿色区域的左边界。而我们接下来要讨论的二分查找模板就是用来 寻找\(C_1\)和\(C_2\)的分界点的。

1.1.1 寻找右边界的二分查找

前面说过，\(C_1\)和\(C_2\)的分界点 一共有两个 ，因此我们的整数二分查找模板也有两个。一个用来查找右边界（即左侧的分界点，对应索引3），一个用来查找左边界（即右侧的分界点，对应索引3）。这里首先介绍查找右边界的模板。

因为查找的是 红色区域的右边界 ，所以先定义一个函数 check(i)，其中参数i是索引。当i位于红色区域，即 \(0\leq i \leq 3\) 时，check(i) 为真；当i位于绿色区域，即\(4\leq i \leq 7\)时，check(i) 为假。

初始时设置左右两个指针分别位于数组的左右两端，每次循环时计算 \(mid=\frac{l+r}{2}\)（至于mid到底取多少稍后会说），然后判断 check(mid) 的值（为实现二分查找， 我们需要确保每次缩小区间时答案都落在区间内 。这样一来，当最终 l == r 时，l 就是我们需要的答案）。如果 check(mid) 为真，说明mid位于红色区域，且mid有可能就是右边界 ，因此接下来令l=mid来缩小查找范围（因为我们要保证缩小后的区间仍然包含答案）；如果 check(mid) 为假，说明mid位于绿色区域，且mid必不可能是红色区域的右边界 ，因为mid最多是索引4，因此令r=mid-1来缩小查找范围。

接下来重点关注mid到底该取多少。如果\(mid=\frac{l+r}{2}\)，其中的除法代表整除，在某一轮循环出现了r-l=1，则\(mid=\frac{2l+1}{2}=l\)。若 check(mid) 为真，则更新后的区间仍然为\([l,r]\)，这就会导致无限循环。事实上，只需要取\(mid=\frac{l+r+1}{2}\)，若 check(mid) 为真，则mid=r，更新后的区间为\([r,r]\)，循环结束。若 check(mid) 为假，则更新后的区间为\([l,l]\)，循环结束。

寻找右边界的二分查找模板：

int right_bound(int l, int r) {
    while (l < r) {
        int mid = (l+r+1) >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

1.1.2 寻找左边界的二分查找

类似1.1.1节中的分析，因为查找的是 绿色区域的左边界 ，所以先定义一个函数 check(i)，其中参数i是索引。当i位于绿色区域，即 \(4\leq i \leq 7\) 时，check(i) 为真；当i位于红色区域，即 \(0\leq i \leq 3\) 时，check(i) 为假。

初始时设置左右两个指针分别位于数组的左右两端，每次循环时计算 \(mid=\frac{l+r}{2}\) （至于mid到底取多少稍后会说），然后判断 check(mid) 的值。如果 check(mid) 为真，说明mid位于绿色区域，且mid有可能就是左边界 ，因此接下来令r=mid来缩小查找范围；如果 check(mid) 为假，说明mid位于红色区域，且mid必不可能是绿色区域的左边界，因为mid最多是索引3，因此令l=mid+1来缩小查找范围。

接下来重点关注mid到底该取多少。如果 \(mid=\frac{l+r}{2}\)，其中的除法代表整除，在某一轮循环出现了r-l=1，则 \(mid=\frac{2l+1}{2}=l\)。若 check(mid) 为真，则更新后的区间为\([l,l]\)，循环结束。若 check(mid) 为假，则更新后的区间为\([r,r]\)，循环结束。综上所述，mid取 \(\frac{l+r}{2}\) 即可。

寻找左边界的二分查找模板：

int left_bound(int l, int r) {
    while (l < r) {
        int mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

二、浮点数二分

2.1 浮点数二分查找模板

相比整数二分，浮点数二分就要简单许多了，因为浮点数二分不涉及到边界问题。

浮点数二分 通常用来求某个数 \(x\) 的近似值（ \(x\) 不易直接求得，例如 \(x=\sqrt{2}\) 等）。由于此时左右两个指针也均为浮点数，所以我们不能直接判断 l == r，而是判断 r - l 是否小于预先设定的精度。

模板如下：

double fsearch(double l, double r, double eps) {
    while(r - l > eps) {
        double mid = (l+r) / 2;
        if(check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

一些注意事项：

若要求精确到小数点后k位，则eps取 \(10^{-(k+2)}\)
若 \(mid\geq x\)，则 check(mid) 为真，否则为假

三、使用STL进行二分查找

3.1 std::binary_search

template< class ForwardIt, class T >
bool binary_search( ForwardIt first, ForwardIt last, const T& value );
```    


该函数用来检查 `[first, last)` 区间内（该区间已排序）是否有数字 **等于** `value`，如果有返回 `true`，否则返回 `false`。

## 3.2 std::lower_bound

```cpp
template< class ForwardIt, class T >
ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value );

该函数用来返回 [first, last) 区间内（该区间已排序） 首个大于等于 value 的元素的迭代器，如果找不到这种元素则返回 last。

3.3 std::upper_bound

1 2	`template< class ForwardIt, class T > ForwardIt upper_bound( ForwardIt first, ForwardIt last, const T& value );`

该函数用来返回 [first, last) 区间内（该区间已排序） 首个大于 value 的元素的迭代器，如果找不到这种元素则返回 last。

3.4 std::equal_range

1
2
3

template< class ForwardIt, class T >
std::pair<ForwardIt, ForwardIt>
    equal_range( ForwardIt first, ForwardIt last, const T& value );

该函数用来返回 [first, last) 区间内（该区间已排序） 所有等于 value 的元素的「范围」。「范围」实际上是由两个迭代器构成的 pair。pair 中的第一个元素是 std::lower_bound 的返回值，pair 中的第二个元素是 std::upper_bound 的返回值。

#二分查找

二分查找模板

https://s1mplebug.github.io/2023/08/06/二分查找模板/

发布于

2023年8月6日

许可协议